Системы счисления

Аддитивные системы счисления

Мультипликативные
системы счисления

Примеры различных
систем счисления

Троичная
система счисления

Восьмеричная
система счисления

Шестнадцатеричная
система счисления

Задачи

Двоичная система счисления

Двоичная система счисления является основной системой представления информации в памяти компьютера.

В этой системе счисления используются две цифры: 0 и 1.

Двоичную цифру называют битом.

Первое опубликованное обсуждение двоичной системы счисления принадлежит испанскому священнику Хуану Карамюэлю Лобковицу ( 1670 г .). Всеобщее внимание к этой системе привлекла статья немецкого математика Готфрида Вильгельма Лейбница, опубликованная в 1703 г . В ней пояснялись двоичные операции сложения, вычитания, умножения и деления. Лейбниц не рекомендовал использовать эту систему для практических вычислений, но подчёркивал её важность для теоретических исследований. Со временем двоичная система счисления становится хорошо известной и получает развитие. Большинство современных электронно-вычислительных машин используют в своей работе именно эту систему чисел.

С помощью двоичной системы кодирования можно зафиксировать любые данные и знания. Это легко понять, если вспомнить принцип кодирования и передачи информации с помощью азбуки Морзе.

Телеграфист, используя только два символа этой азбуки - точки и тире, может передать практически любой текст.

Объём памяти компьютера измеряется в байтах. Каждый байт может выражать букву, число, пробел, знак препинания или какой-либо другой символ. Количество символов, которые компьютер может хранить в оперативной памяти, меняется в широких пределах от вида компьютера и его модели.

Объём памяти, хотя он и измеряется в байтах, обычно выражается в килобайтах. Слово "килобайт", вообще говоря, означает "1000 байт". (Напомним, что приставка "кило" означает "тысяча".)

Фактически же килобайт равен 1024 байтам: 1 Кбайт = 1024 байт.

Компьютер с объёмом памяти в 64 К может хранить 64 х 1024 = 65536 символов.

Объём памяти первых микрокомпьютеров составлял всего лишь 2 Кб. Нынешние компьютеры имеют объём памяти 128, 256, 512, 1024 Мб и более

Объём памяти новейших компьютеров так велик, что она выражается в гигабайтах, т. е. в миллиардах байтов.

1 Мбайт = 1024 Кбайт = 1 048 576 байт.

Итак, каждый символ алфавитно-цифровой информации представляется в компьютере кодом из восьми двоичных цифр. Следовательно, каждый символ в компьютере имеет код объёмом 1 байт.

Информатика и образование

имеет в двоичной форме объём 25 байт: 23 буквы и 2 символа "пробел" по 1 байту.

Пример. Измерим в байтах объём текстовой информации в книге из 258 страниц, если на одной странице размещается в среднем 45 строк по 60 символов (включая пробелы). Один символ в двоичной форме содержит 1 байт. Строка будет содержать 61 байт, учитывая и служебный символ окончания строки. Тогда

61 байт * 45 строк = 2745 байт.

Так как в книге 258 страниц текста и на каждой странице в среднем по 2745 байт информации, то объём алфавитно-цифровой информации в книге

2745 байт * 258 страниц = 708210 байт " 692 Кбайт

Таким образом, текст книги имеет объём около 692 Кбайт.

Перевод чисел

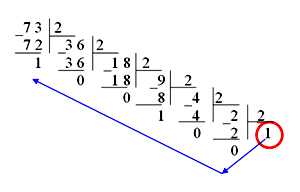
Для перевода десятичного числа в двоичное надо разделить его на 2 и собрать остатки, начиная с последнего частного.

73₁₀ = 1001001₂

А вот как происходит перевод двоичного числа в десятичное:

ДРОБНЫЕ ЧИСЛА В ДВОИЧНОЙ СИСТЕМЕ СЧИСЛЕНИЯ

В любой системе счисления нужно уметь представлять не только целые числа, но и дробные. С математической точки зрения это ординарная задача, которая давно решена. Однако с точки зрения компьютерной техники это далеко не тривиальная проблема, во многом связанная с архитектурой компьютера. Ресурсы компьютеров не бесконечны, и основной трудностью является представление периодических и непериодических дробей. Следовательно, такие дроби следует округлять, задавать класс точности участвующих (и могущих появиться в результате вычислений!) чисел без потери точности вычислений, а также следить за тем, чтобы потеря точности не произошла при переводе чисел из одной системы счисления в другую. Особенно важно аккуратно производить вычисления при операциях с плавающей точкой.

Запишем формулу представления дробного числа в позиционной системе счисления:

A_p = a_n-1·p^n-1+a_n-2·p^n-2 + ... + a₁·p¹+a₀·p⁰ +a_-1·p^-1+a_-2·p^-2 + ... + a_-m·p^-m,       

В случае десятичной системы счисления получим:

24,73₁₀ = (2·10¹+4·10⁰+7·10^-1+3·10^-2)₁₀

Перевод дробного числа из двоичной системы счисления в десятичную производится по следующей схеме:

101101,101₂ = (1·2⁵+0·2⁴+1·2³+1·2²+0·2¹+1·2⁰+1·2^-1+0·2^-2+1·2^-3)₁₀=45,625₁₀

Перевод дробного числа из десятичной системы счисления в двоичную осуществляется по следующему алгоритму:

·  Вначале переводится целая часть десятичной дроби в двоичную систему счисления;

·  Затем дробная часть десятичной дроби умножается на основание двоичной системы счисления;

·  В полученном произведении выделяется целая часть, которая принимается в качестве значения первого после запятой разряда числа в двоичной системе счисления;

·  Алгоритм завершается, если дробная часть полученного произведения равна нулю или если достигнута требуемая точность вычислений. В противном случае вычисления продолжаются с предыдущего шага.

Пример: Требуется перевести дробное десятичное число 206,116 в дробное двоичное число.

Перевод целой части дает 206₁₀=11001110₂ по ранее описанным алгоритмам; дробную часть умножаем на основание 2, занося целые части произведения в разряды после запятой искомого дробного двоичного числа:

.116 • 2 = 0.232

.232 • 2 = 0.464

.464 • 2 = 0.928

.928 • 2 = 1.856

.856 • 2 = 1.612

.612 • 2 = 1.224

.224 • 2 = 0.448

.448 • 2 = 0.896

.896 • 2 =1.792

.792 • 2 = 1.584

и т.д.

Получим: 206,116₁₀=11001110,0001110011₂

Таблицу степеней первых восьми отрицательных степеней двойки 

Отрицательные числа

Перейдем теперь к вопросу представления отрицательных чисел. Для определенности рассмотрим тип byte, в котором любое число занимает ровно восемь бит. Из записи в двоичной системе счисления равенства (- 1) + 1 = 0 легко найти, какой вид должно иметь неизвестное нам пока двоичное представление xxxxxxxx числа - 1:

    xxxxxxxx + 00000001 = 00000000      

Ясно, что на месте символов xxxxxxxx должно быть расположено число 11111111. Правильным результатом при этом, конечно, следовало бы считать 100000000, а не 00000000, но ведь мы имеем дело с типом byte и, так как результат обязан разместиться в байте, единица <<исчезает>>.

Итак, число - 1 должно кодироваться как 11111111. Дальнейшее уже совсем просто: для получения - 2 нужно - 1 уменьшить на единицу, что даст 11111110; число - 3 представляется как 11111101 и т.д.

Отрицательные числа всегда имеют в своем двоичном представлении единицу в самом старшем разряде, который поэтому называют знаковым, а абсолютная величина кодируемого числа получается как двоичное дополнение остальных бит (нули нужно заменить на единицы и наоборот), увеличенное на один.

Легко видеть, что при этом самым маленьким отрицательным числом, которое принадлежит типу byte, является число - 128 (двоичное представление 10000000), а самым большим -- число 127 (представление 01111111). Все представимыe числа (а их 256) в данном случае могут быть получены как пересечение двух множеств: множества Z всех целых чисел и отрезка [ - 128; 127 ].

Интересным является следующее наблюдение: если число 01111111 увеличить на единицу, то получится 10000000, что означает следующее:

127 + 1 = - 128 !!!

Итак, множество элементов типа byte можно представлять себе в виде свернутого в кольцо отрезка
[ - 128; 127 ].

То, что для элементов множества , являющегося машинным аналогом Z, нарушено фундаментальное свойство целых чисел X + 1 > X, способно привести к различным невероятным на первый взгляд результатам, однако гораздо более странные вещи происходят при работе с вещественными числами.

Двоичная арифметика

Над числами в двоичной системе счисления можно выполнять арифметические действия.

При этом используются следующие таблицы:

Рассмотрим примеры:

1 1 0 1 0 12 + 1 1 0 1 12
1 1 0 1 12 - 1 1 0 12
1 1 0 1 12 * 1 0 12

Для деления в двоичной системе счисления нужно уметь сравнивать числа (определять, какое больше) и хорошо вычитать. Посмотри деление на анимированном примере

Пример:

Еще несколько примеров:
Несколько примеров для тренировки: